Nombor bulat ialah blok binaan asas matematik, mewakili kuantiti lengkap tanpa pecahan atau perpuluhan. Bermula dari sifar dan melanjutkan tak terhingga ke arah positif, Nombor Penuhmerangkumi semua integer positif dan sifar. Nombor ini menemui pelbagai aplikasi dalam mengira, mengukur dan menyatakan kuantiti. Mereka meletakkan asas untuk pelbagai operasi matematik, daripada penambahan dan penolakan asas kepada pengiraan yang kompleks. Nombor Penuh berfungsi sebagai alat penting untuk memahami konsep matematik dan menyelesaikan masalah dunia sebenar. Sebagai komponen penting dalam sistem nombor, ia merapatkan jurang antara konsep matematik abstrak dan senario harian yang praktikal. Dalam artikel ini kita akan membincangkan tentang Nombor Bulat

Anda Juga Boleh Suka- Nombor Perdana 1 Hingga 100
Nombors Bulat
Apakah Yang Kami Maksudkan Dengan Nombors Bulat?
Dalam kehidupan seharian kita, kita sering menggunakan mengira nombor seperti 1, 2, 3, dan seterusnya. Nombor Penuh merangkumi nombor pengiraan asas ini serta sifar. Dalam matematik, mengira nombor dirujuk sebagai nombor asli. Oleh itu, kita boleh menerangkan Nombor Penuh sebagai set yang merangkumi semua nombor asli dan sifar. Nombor Penuh merangkumi integer positif bersama-sama dengan sifar.
Nombor Penuh terdiri daripada nombor asli bermula dari 1 dan seterusnya.
Sekarang, mari kita periksa beberapa contoh Nombor Penuh.
[id jadual=21 /]
Pengumpulan Nombor Penuh dilambangkan dengan huruf ‘W’.
W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …}
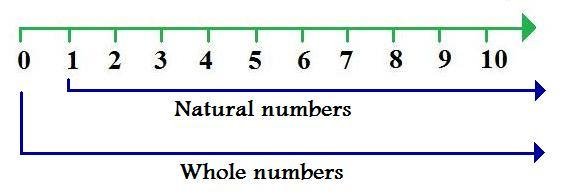
Nombors Bulat Diwakili Pada Garis Nombor:
Susunan Nombor Penuh boleh diwakili pada garis nombor, seperti yang digambarkan di bawah.
Nombors Bulat Terkecil Dan Terbesar
Di antara Nombor Penuh, 0 adalah yang terkecil. Ia memegang kedudukan yang unik kerana ia tidak mempunyai pendahulu atau nombor sebelumnya. Walau bagaimanapun, tiada Nombor Penuh ‘terbesar’ yang pasti.
Sifat Nombors Bulat:
Operasi aritmetik asas penambahan, penolakan, pendaraban dan pembahagian menghasilkan empat sifat utama dalam alam Nombor Penuh.
1. Harta Penutupan:
Jumlah dan hasil darab dua Nombor Penuh sentiasa menghasilkan Nombor Penuh lain, menjadikan operasi tambah dan darab ditutup dalam set nombor bulat.
Sebagai contoh, pertimbangkan 5 dan 8:
5 + 8 = 13 (Nombor Penuh)
5 × 8 = 40 (Nombor Penuh)
2. Harta Komutatif:
Keputusan menambah atau mendarab Nombor Penuh kekal tidak berubah walaupun urutan nombor ditukar.
Sebagai contoh, ambil 2 dan 7:
2 + 7 = 7 + 2 = 9
2 × 7 = 7 × 2 = 14
Sifat ini berlaku untuk kedua-dua penambahan dan pendaraban.
3. Harta Bersekutu:
Pengumpulan Nombor Penuh semasa penambahan atau pendaraban tidak mempengaruhi jumlah atau hasil darab.
Sebagai ilustrasi, pertimbangkan 2, 3, dan 4:
2 + (3 + 4) = 2 + 7 = 9
(2 + 3) + 4 = 5 + 4 = 9
Oleh itu, 2 + (3 + 4) = (2 + 3) + 4
Begitu juga, ambil 2, 3, dan 4 sekali lagi:
2 × (3 × 4) = 2 × 12 = 24
(2 × 3) × 4 = 6 × 4 = 24
Oleh itu, 2 × (3 × 4) = (2 × 3) × 4
4. Harta Pengedaran:
Mendarab Nombor Penuh ke atas jumlah atau perbezaan Nombor Penuh lain menunjukkan sifat taburan, membantu dalam menyelesaikan persamaan.
Pertimbangkan 9, 11, dan 6:
9 × (11 + 6) = 9 × 17 = 153
(9 × 11) + (9 × 6) = 99 + 54 = 153
Kesimpulannya, 9 × (11 + 6) = (9 × 11) + (9 × 6)
Membezakan Antara Nombor Bulat Dan Nombor Asli:
Berdasarkan perbezaan ini, menjadi jelas bahawa semua Nombor Penuh kecuali 0 adalah, sebenarnya, nombor asli. Dalam istilah yang lebih mudah, kita boleh membuat kesimpulan bahawa koleksi nombor asli sesuai dalam alam Nombor Penuh.
Fakta-Fakta Yang Menyeronokkan
- Tidak ada Nombor Penuh yang ‘terbesar’.
- Setiap Nombor Penuh, kecuali 0, mempunyai nombor tepat di hadapannya.
- Nombor antara dua Nombor Penuh, seperti perpuluhan atau pecahan, tidak dianggap nombor bulat.
Latihan Masalah Pada Nombor Bulat
1. Apa Yang Berlaku Selepas 1099?
a) 1100, 1101, 1102
b) 1090, 1010, 1100
c) 1101, 1102, 1103
d) 1000, 1001, 1002
2. Berapakah Bilangan Nombor Bulat Antara 22 Dan 35?
a) 20
b) 22
c) 12
d) 14
3. Antara Berikut, Yang Manakah Bersamaan Dengan 636 × 102?
a) 636 × (10 + 2)
b) (600 + 30) × 102
c) 636 × (100 + 2)
d) (600 + 2) × 102
4. Kira 6 × (40 + 2).
a) 172
b) 252
c) 272
d) 300
Pertanyaan Biasa Mengenai Nombor Bulat:
S1. Tunjukkan Beberapa Nombor Yang Merupakan Nombor Bulat Dan Ada Yang Bukan.
J1.Nombor Penuh ialah nombor positif yang tidak mempunyai sebarang pecahan atau perpuluhan, termasuk sifar.
Contoh: 0, 1, 2, 3, 4, 5, 6, 7
Bukan contoh: 3, 2.7, atau 3 ½
S2. Bolehkah Kita Mewakili 1/2 Sebagai Nombor Bulat?
J2.Tidak, tidak mungkin untuk menyatakan pecahan yang disediakan sebagai Nombor Penuh. Nombor Penuh tidak termasuk pecahan atau bahagian perpuluhan.
Kita boleh membundarkan ½ atau 0.5 kepada sama ada 1 atau 0.
S3. Apakah Tujuan Orang Ada Untuk Menggunakan Nombor Bulat?
J3. Nombor Penuh adalah seperti blok binaan yang membantu kita memahami nombor yang lebih besar seperti perpuluhan, pecahan dan jenis lain. Apabila kita membundarkan nombor perpuluhan kepada Nombor Penuh, ia menjadikan matematik lebih mudah dan cepat.