Nombor Fibonacci , urutan integer di mana setiap nombor adalah jumlah dua nombor sebelumnya (bermula dari 0 dan 1), telah memikat hati ahli matematik dan peminat di Malaysia. Muncul sebagai konsep asas dalam matematik, nombor ini mendedahkan corak merentas pelbagai bidang, daripada pertumbuhan alam semula jadi kepada pasaran kewangan. Lingkaran Fibonacci yang menarik, dikaitkan dengan jujukan, mempamerkan sambungan yang menarik kepada nisbah emas. Di Malaysia, seperti di seluruh dunia, penerokaan nombor ini terus menimbulkan rasa ingin tahu, memacu penyelidikan dan aplikasi dalam pelbagai domain seperti teknologi, seni dan kewangan. Dalam artikel ini kita akan membincangkan tentang Nombor Fibonacci

Anda Juga Mungkin Suka- Maksud Nombor Dalam Bahasa Cina
Nombor Fibonacci
Jujukan Fibonacci:
Urutan Fibonacci ialah senarai nombor khas yang bermula dengan 0 dan 1. Setiap nombor baharu dibuat dengan menambah dua nombor sebelum itu. Jadi, ia berlaku seperti ini: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, dan teruskan. Ia dinamakan sempena seorang lelaki bernama Fibonacci dari Itali yang menunjukkannya kepada dunia suatu masa dahulu. Urutan ini seperti corak rahsia yang terdapat dalam alam semula jadi. Ia muncul dalam cara bunga matahari, aster, brokoli, dan cengkerang tumbuh dalam bentuk lingkaran. Mempelajari tentang jujukan ini membantu kami memahami lebih lanjut tentang cara ia muncul dalam pelbagai perkara dalam alam semula jadi.
Apakah Jujukan Fibonacci?
Urutan Fibonacci ialah senarai nombor yang tidak berkesudahan seperti 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, dan seterusnya. Ringkasnya, setiap nombor dalam urutan ini adalah hasil daripada menambah dua nombor sebelum itu. Dua nombor pertama dalam jujukan ialah 0 dan 1. Kami memanggil nombor ini dalam jujukan “Nombor Fibonacci.” Berikut ialah 20 nombor pertama dalam urutan:
| Terma Jujukan Fibonacci | |
|---|---|
| F0 = 0 | F10 = 55 |
| F1 = 1 | F11 = 89 |
| F2 = 1 | F12 = 144 |
| F3 = 2 | F13 = 233 |
| F4 = 3 | F14 = 377 |
| F5 = 5 | F15 = 610 |
| F6 = 8 | F16 = 987 |
| F7 = 13 | F17 = 1597 |
| F8 = 21 | F18 = 2584 |
| F9 = 34 | F19 = 4181 |
Di sini, kita boleh perhatikan bahawa bagi setiap n yang lebih besar daripada 1, nilai Fn ditemui dengan menambah Fn-1 dan Fn-2. Sebagai contoh:
– F2 ialah hasil tambah bagi F1 dan F0.
– F3 ialah hasil tambah bagi F2 dan F1.
– F4 ialah hasil tambah bagi F3 dan F2, dan seterusnya.
Kepentingan Jujukan Fibonacci dilihat dari cara ia muncul dalam alam semula jadi dan cara ia berguna dalam bidang yang berbeza seperti matematik, sains, seni dan perkara wang. Urutan ini ditunjukkan dalam cara daun tumbuh pada batang, cara pokok berpecah menjadi dahan, dan bentuk cengkerang dan galaksi yang berpintal. Ia juga digunakan untuk menerangkan cara populasi berkembang, corak pasaran saham dan banyak lagi.
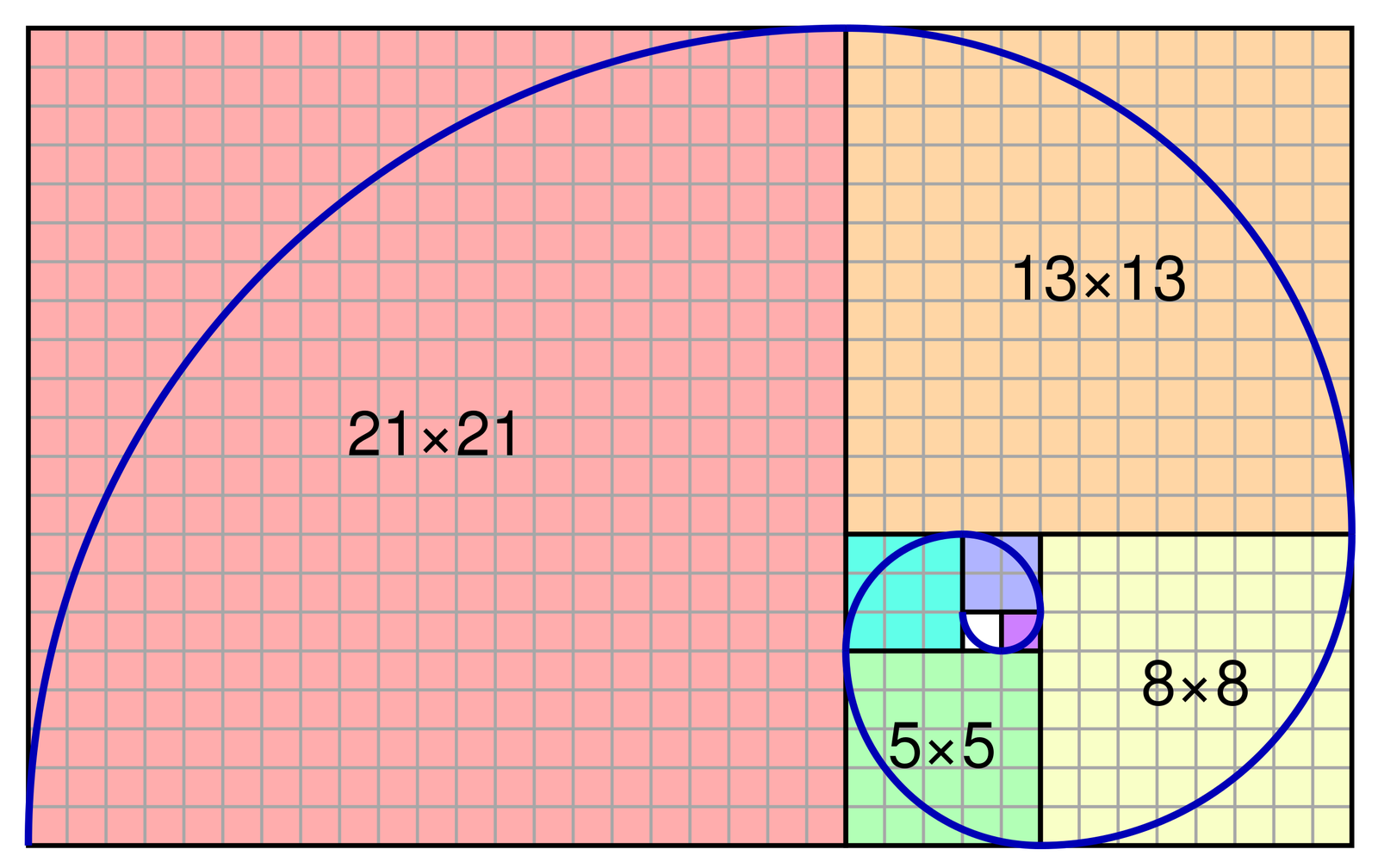
Lingkaran Dihubungkan Dengan Jujukan Fibonacci
Lingkaran Fibonacci ialah reka bentuk geometri yang berasal daripada jujukan Fibonacci. Corak ini dibentuk dengan melukis suku bulatan bersambung dalam satu siri segi empat sama, bersaiz berdasarkan jujukan Fibonacci.
Lingkaran bermula dengan segi empat sama kecil, diikuti dengan yang lebih besar yang disambungkan kepadanya. Petak seterusnya menggunakan saiz daripada jumlah dua petak sebelumnya. Proses ini berterusan, dengan setiap suku bulatan dipasang dengan kemas di dalam petak seterusnya, menyebabkan corak berputar ke luar tanpa henti. Apabila nombor dalam jujukan Fibonacci meningkat, nisbah menghampiri nisbah emas (sekitar 1.618).
Dalam lingkaran Fibonacci ini, setiap dua sebutan berturut-turut bagi jujukan Fibonacci mewakili panjang dan lebar segi empat tepat. Mari kita mengira nisbah setiap dua sebutan berturut-turut bagi jujukan Fibonacci dan lihat bagaimana ia membentuk nisbah emas.
- F 2 /F 1 = 1/1 = 1
- F 3 /F 2 = 2/1 = 2
- F 4 /F 3 = 3/2 = 1.5
- F 5 /F 4 = 5/3 = 1.667
- F 6 /F 5 = 8/5 = 1.6
- F 7 /F 6 = 13/8 = 1.625
- F 8 /F 7 = 21/13 = 1.615
- F 9 /F 8 = 34/21 = 1.619
- F 10 /F 9 = 55/34 = 1.617
- F 11 /F 10 = 89/55 = 1.618 = Nisbah Emas
Jadi, apabila segi empat tepat itu benar-benar besar, sisinya menjadi sangat hampir untuk membuat segi empat tepat emas.
Dalam kata mudah, lingkaran Fibonacci dan nisbah emas adalah idea menarik yang berkait rapat dengan Jujukan Fibonacci. Ia banyak muncul dalam alam semula jadi dan perkara yang dicipta oleh orang ramai. Orang ramai terus mengkaji dan belajar tentang mereka di kawasan yang berbeza.
Formula Untuk Jujukan Fibonacci
Formula untuk jujukan Fibonacci, yang dilambangkan sebagai “Fn,” ditentukan menggunakan formula langkah demi langkah. Kami mulakan dengan F0 = 0 dan F1 = 1, dan kemudian kami menggunakan formula berikut untuk mengetahui nilai Fn. Inilah rupa formula Fibonacci:
Fn = Fn-1 + Fn-2, dengan n > 1. Di sini,
Fn bermaksud nombor ke (n+1) dalam jujukan, dan
Fn-1 dan Fn-2 bermaksud dua nombor sebelum dalam jujukan.
Formula untuk jujukan Fibonacci membantu kami mencari istilah baharu dengan menambah dua istilah sebelumnya. Sebagai contoh, kerana kita tahu dua sebutan pertama ialah 0 dan 1, kita boleh menggunakan formula untuk mencari sebutan ke-3 seperti ini:
F3 = F1 + F2 = 0 + 1 = 1.
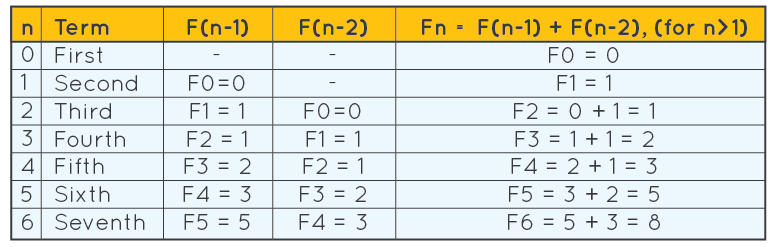
Dengan cara yang sama, kita boleh menggunakan formula untuk mencari istilah lain dalam jujukan Fibonacci, seperti yang digambarkan dalam rajah di bawah.
Sila faham bahawa dalam konteks ini, F0 dirujuk sebagai istilah awal, bukan F1. Oleh itu, dalam perwakilan ini, Fn menandakan sebutan (n + 1) dalam jujukan Fibonacci.
Sifat-Sifat Jujukan Fibonacci:
Urutan Fibonacci mempunyai beberapa perkara menarik mengenainya.
1) Nombor Fibonacci berkaitan dengan sesuatu yang dipanggil nisbah emas. Kita boleh menyusun sebarang nombor Fibonacci menggunakan idea nisbah emas ini. Ia kelihatan seperti ini: Fn = (Φ^n – (1-Φ)^n) / √5. Formula khas ini kadangkala dipanggil “formula Binet.” Dalam formula ini, Φ ialah nisbah emas, iaitu kira-kira 1.618034.
Sebagai contoh, jika kita ingin mencari nombor ke-7 (F7) dalam jujukan, kita menggunakan formula seperti ini: F7 = [(1.618034)^7 – (1-1.618034)^7] / √5 = 13.
2) Semasa kita terus bergerak mengikut urutan Fibonacci, hubungan antara satu nombor dan nombor seterusnya semakin hampir dengan nisbah emas.
| A | B | A/B |
|---|---|---|
| 2 | 3 | 1.5 |
| 3 | 5 | 1.6 |
| 5 | 8 | 1.6 |
| 8 | 13 | 1.625 |
| 144 | 233 | 1.618055555555556 |
| 233 | 377 | 1.618025751072961 |
Anda boleh membuat anggaran nombor Fibonacci seterusnya dengan mendarab nombor sebelumnya dengan nisbah emas (sekitar 1.618034). Sebagai contoh, jika anda mempunyai nombor 13 dalam urutan dan melakukan 13 × 1.618034…, anda mendapat 21.034442. Ini meramalkan nombor Fibonacci seterusnya selepas 13, iaitu 21.
2) Lihat dengan teliti pada urutan untuk menemui satu lagi corak yang menarik. Setiap nombor ketiga dalam urutan (bermula dari nombor kedua) adalah hasil darab dengan 2. Begitu juga, setiap nombor keempat (bermula dari nombor ketiga) adalah hasil darab dengan 3, dan setiap nombor kelima (bermula dari nombor kelima nombor) ialah hasil darab dengan 5, dan seterusnya.
3) Urutan Fibonacci juga berfungsi dengan nombor negatif. Kami menyatakannya seperti ini: Fn = (-1)^n+1 × Fn. Sebagai contoh, jika anda mempunyai F-4, anda boleh menggunakan (-1)^5 × F4, yang memudahkan kepada (-1)^3 = -3.
4) Apabila anda ingin menambah n sebutan bagi jujukan Fibonacci, anda boleh menggunakan formula ini: Σi=0n Fi = Fn+2 – F2 (atau) Fn+2 – 1, dengan Fn ialah nombor Fibonacci ke-n. Ingat, urutan bermula dari F0.
Sebagai contoh, jika anda menjumlahkan 10 nombor pertama dalam jujukan, ia seperti mencari nombor ke-12 dan kemudian mengambil 1. Jadi, 89 – 1 = 88. Kita boleh menulis ini sebagai Σi=0^9 Fi = F11 – 1 = 89 – 1 = 88.
5) Urutan Fibonacci disambungkan kepada idea matematik lain, seperti nombor Lucas dan segi tiga Pascal.
Kegunaan Jujukan Fibonacci:
Urutan Fibonacci muncul dalam pelbagai bidang, termasuk alam semula jadi, muzik, dan juga tubuh manusia.
– Ia digunakan untuk mencipta corak dan perkadaran nombor yang menggembirakan dalam muzik.
– Ia digunakan dalam pengekodan, yang membantu dengan algoritma komputer, memautkan sistem selari dan teragih.
– Urutan muncul dalam pelbagai bidang saintifik seperti fizik bertenaga tinggi, mekanik kuantum dan kriptografi.
– Ia digunakan untuk menerangkan banyak perkara dalam biologi, seperti cara tumbuhan tumbuh dan cara daun disusun pada batang.
– Urutan juga digunakan dalam kewangan untuk melihat arah aliran dalam harga saham dan maklumat kewangan lain.
Anda boleh mencuba kalkulator Fibonacci, yang membantu mengetahui Jujukan Fibonacci. Lihat beberapa contoh yang telah diselesaikan untuk mendapatkan idea yang lebih baik tentang cara formula Fibonacci berfungsi.