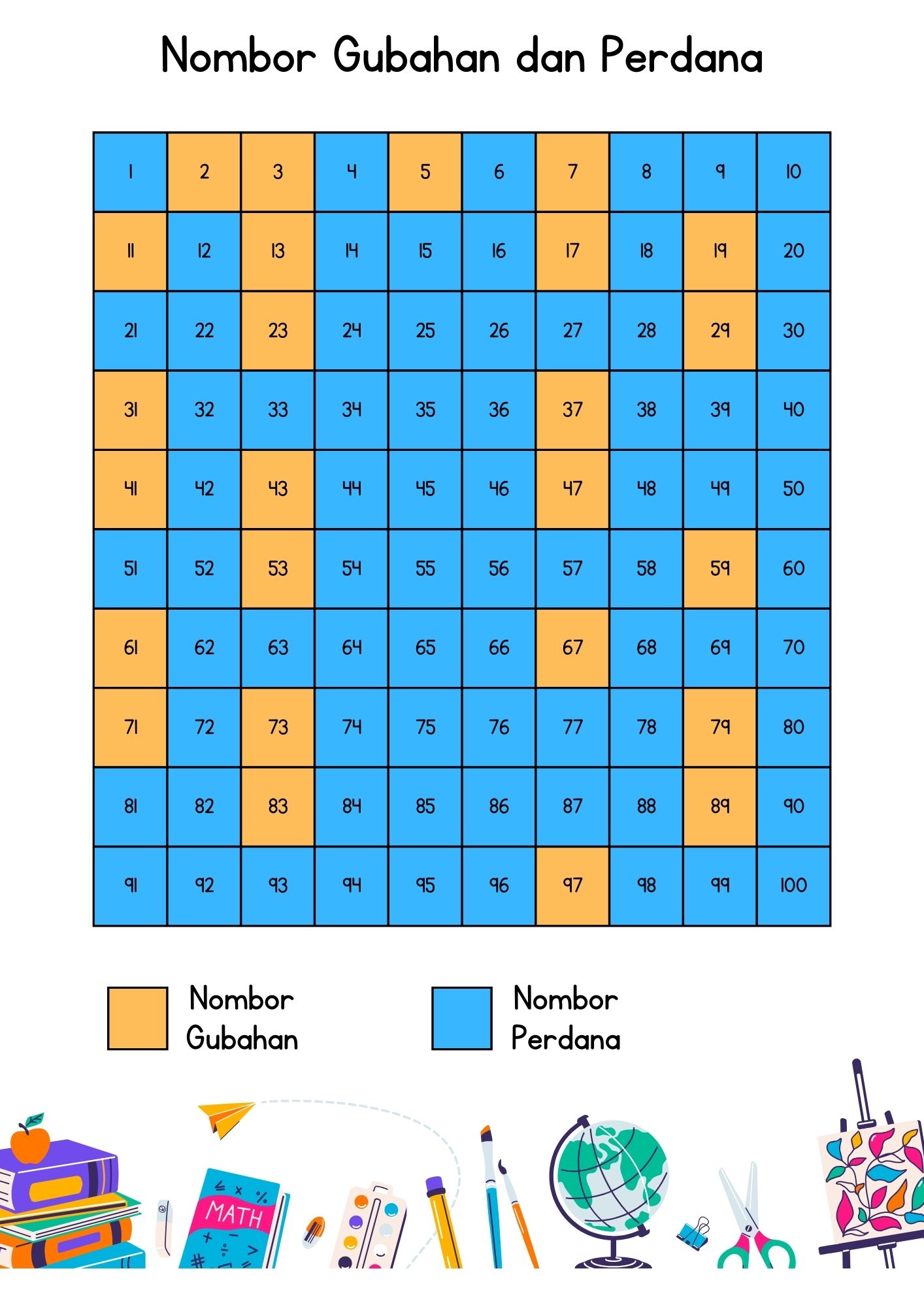
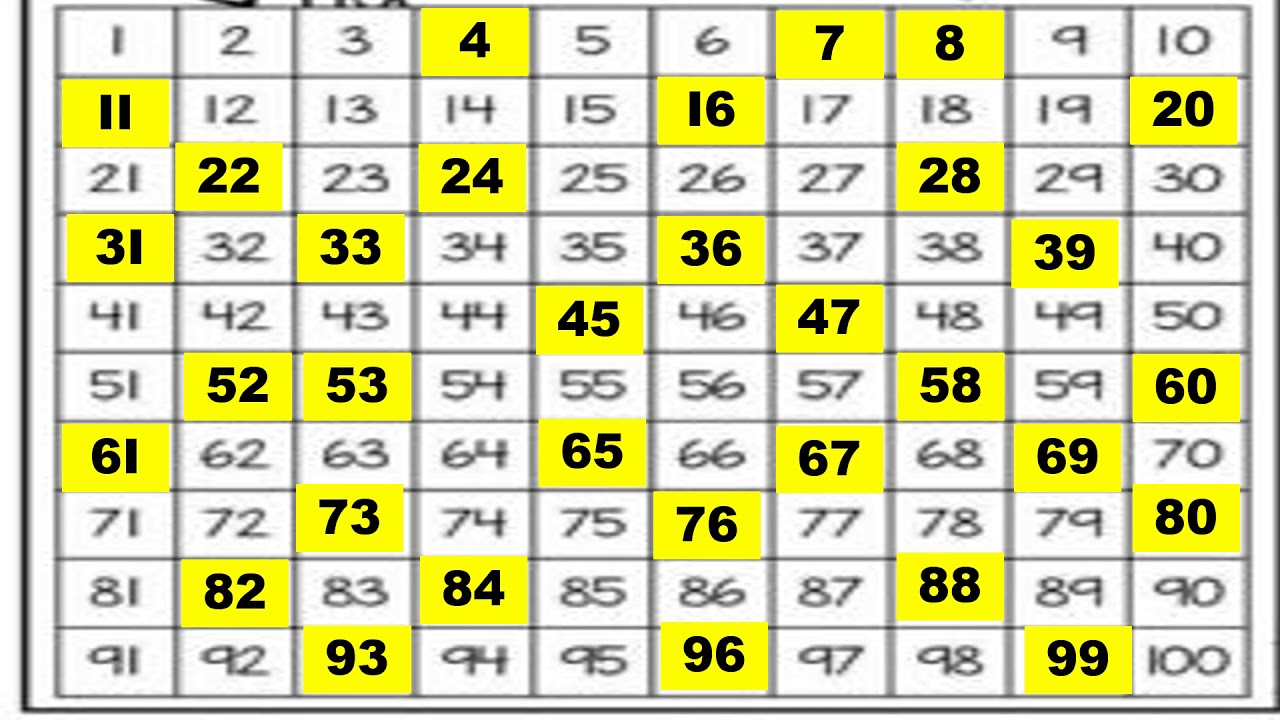
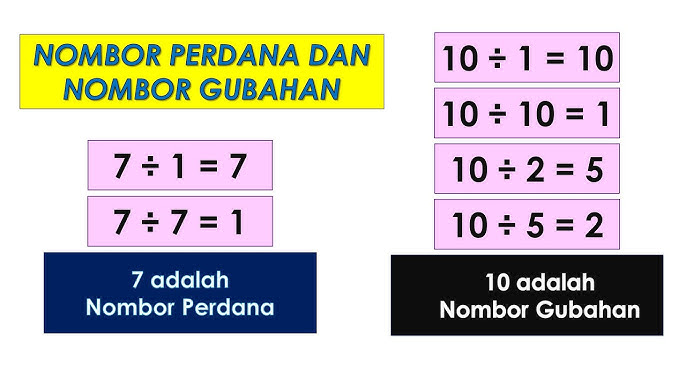
Nombor Gubahan adalah konsep yang menarik dalam matematik. Nombor ini lebih daripada sekadar nombor pengiraan biasa seperti 1, 2, 3, dan seterusnya. Mereka mempunyai sifat istimewa yang membezakan mereka – mereka boleh dibahagikan dengan nombor selain daripada hanya 1 dan diri mereka sendiri. Dalam erti kata lain, mereka mempunyai lebih daripada dua faktor. Sebagai contoh, 4 ialah nombor komposit kerana ia boleh dibahagikan sama rata dengan 2. Tidak seperti nombor perdana, yang hanya mempunyai dua faktor (1 dan dirinya sendiri), nombor komposit mempunyai pelbagai faktor. Memahami nombor komposit membantu kami meneroka dunia nombor yang kaya dan ciri uniknya. Dalam artikel ini kita akan membincangkan tentang Nombor Gubahan
Nombor Gubahan
Nombor komposit ialah nombor bulat yang lebih besar daripada sifar dan mempunyai pembahagi positif selain daripada satu atau dirinya sendiri. Dalam istilah mudah, jika anda mempunyai integer n lebih besar daripada sifar, dan anda boleh mencari dua integer a dan b (kedua-duanya lebih besar daripada 1 dan kurang daripada n) yang boleh didarab untuk memberikan n, maka n ialah nombor komposit. Dalam dunia integer, setiap nombor yang lebih besar daripada satu adalah sama ada nombor perdana atau nombor komposit. Nombor satu adalah unik – ia tidak termasuk dalam kategori utama atau komposit. Sebagai contoh, nombor 14 adalah komposit kerana anda boleh mendarab 2 dan 7 untuk mendapatkan 14. Walau bagaimanapun, nombor seperti 2 dan 3 bukan komposit kerana ia hanya boleh dibahagikan dengan 1 dan sendiri.
105 Nombor Komposit Pertama (Jujukan A002808 Dalam OEIS) Ialah:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 102, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 125, 18 33, 134, 135, 136, 138, 140.
Setiap nombor komposit boleh dinyatakan sebagai hasil darab dua atau lebih nombor perdana (tidak semestinya berbeza). Tambahan pula, perwakilan ini adalah unik kecuali untuk susunan faktor. Konsep asas ini dikenali sebagai teorem asas aritmetik.
Definisi Nombor Komposit:
Nombor komposit ialah integer bukan negatif yang mempunyai pembahagi selain daripada satu dan dirinya sendiri. Dalam erti kata lain, nombor ini boleh dibahagikan sama rata dengan nombor selain daripada hanya satu dan nombor itu sendiri. Sifat unik ini membezakannya daripada nombor perdana
1. Integer Bukan Negatif:
Nombor komposit ialah nombor bulat positif, bermakna ia lebih besar daripada atau sama dengan sifar. Ia adalah sebahagian daripada set nombor yang merangkumi 0, 1, 2, 3, dan seterusnya.
2. Pembahagi:
Pembahagi nombor ialah nombor bulat yang boleh dibahagikan sama rata kepada nombor itu tanpa meninggalkan baki. Sebagai contoh, pembahagi 6 ialah 1, 2, 3, dan 6, kerana ia boleh membahagi 6 sama rata.
3. Selain Daripada Satu Dan Sendiri:
Apa yang membezakan nombor komposit daripada nombor lain ialah ia mempunyai pembahagi selain daripada satu dan nombor itu sendiri. Dalam erti kata lain, terdapat nombor bulat yang boleh membahagi nombor komposit tanpa sama dengan satu atau nombor itu sendiri.
4. Pembahagian Sekata:
Nombor komposit boleh dibahagikan kepada berbilang nombor bulat tanpa sebarang baki. Sebagai contoh, 6 boleh dibahagikan sama rata dengan 2 dan 3.
5. Berbeza Daripada Nombor Perdana:
Sifat unik ini membezakan nombor komposit daripada nombor perdana. Nombor perdana hanya mempunyai dua pembahagi yang berbeza: satu dan diri mereka sendiri. Nombor komposit pula mempunyai lebih daripada dua pembahagi kerana keupayaannya untuk dibahagikan dengan nombor selain daripada satu dan diri mereka sendiri.
Faktor Pembeza: Komposit Lwn Nombor Perdana
Perbezaan Antara Nombor Komposit dan Perdana:
1. Definisi dan Sifat:
– Nombor Komposit: Ini ialah nombor bulat yang mempunyai lebih daripada dua pembahagi positif, termasuk 1 dan diri mereka sendiri.
– Nombor Perdana: Ini ialah nombor bulat yang mempunyai dua pembahagi positif yang berbeza: 1 dan diri mereka sendiri.
2. Kebolehbahagiaan:
– Nombor Komposit: Mereka boleh dibahagikan dengan lebih daripada dua nombor – pembahaginya tidak terhad kepada 1 dan nombor itu sendiri.
– Nombor Perdana: Mereka hanya boleh dibahagikan dengan 1 dan nombor itu sendiri tanpa meninggalkan sebarang baki.
3. Faktor:
– Nombor Komposit: Mereka mempunyai pelbagai faktor yang boleh membahagikannya sama rata, menyumbang kepada pembahagi berbilang mereka.
– Nombor Perdana: Mereka hanya mempunyai dua faktor – 1 dan nombor itu sendiri, yang menjadikannya unik dalam kebolehbahagiaannya.
4. Komposisi Berganda:
– Nombor Komposit: Ia boleh dinyatakan sebagai hasil darab dua atau lebih nombor bulat yang lebih kecil (faktor).
– Nombor Perdana: Mereka tidak boleh dipecahkan kepada hasil darab nombor bulat yang lebih kecil selain daripada 1 dan diri mereka sendiri.
5. Ujian Kebolehbahagiaan:
– Nombor Komposit: Dengan memeriksa faktor nombor dan mencari pembahagi selain daripada 1 dan nombor itu sendiri, anda boleh mengenal pasti sama ada ia adalah komposit.
– Nombor Perdana: Jika nombor mempunyai dua faktor (1 dan dirinya sendiri), ia adalah perdana. Jika tidak, ia tidak.
6. Contoh:
– Nombor Komposit: Contohnya termasuk 4, 6, 8, 9, 10, dsb., yang semuanya boleh dibahagikan dengan nombor selain daripada 1 dan sendiri.
– Nombor Perdana: Contohnya termasuk 2, 3, 5, 7, 11, dsb., yang hanya mempunyai dua pembahagi yang berbeza.
7. Kepentingan Matematik:
– Nombor Komposit: Nombor ini penting dalam teori nombor dan pelbagai aplikasi matematik kerana pembahagiannya yang pelbagai rupa.
– Nombor Perdana: Mereka memainkan peranan penting dalam kriptografi, teori nombor dan pemfaktoran perdana kerana sifat uniknya.
8. Peranan Dalam Matematik:
– Nombor Komposit: Mereka memberikan pemahaman yang lebih mendalam tentang hubungan dan corak nombor, menyumbang kepada pandangan komprehensif tentang matematik.
– Nombor Perdana: Kepentingan mereka meluas ke pelbagai bidang matematik dan aplikasi dunia sebenar, seperti algoritma penyulitan.
Perdana Atau Komposit: Sifat Perduaan
Dua Kategori Berbeza:
Semua integer yang lebih besar daripada satu jatuh ke dalam salah satu daripada dua kategori tertentu: nombor perdana atau nombor komposit.
Nombor Perdana:
-
- Nombor perdana ialah integer yang hanya mempunyai dua pembahagi positif yang berbeza – 1 dan diri mereka sendiri.
- Mereka unik dalam harta boleh bahagi mereka, menjadikannya menonjol antara integer lain.
Nombor Komposit:
-
- Nombor komposit ialah integer yang mempunyai lebih daripada dua pembahagi positif.
- Mereka boleh dibahagikan sama rata dengan nombor selain daripada 1 dan diri mereka sendiri.
Mengenalpasti Nombor Komposit
Proses Pengenalan:
-
- Untuk mengenal pasti nombor komposit, kami mencari nombor yang boleh dibahagikan sama rata oleh sekurang-kurangnya dua pembahagi selain daripada satu dan nombor itu sendiri.
Mencari Pelbagai Pembahagi:
-
- Ciri utama nombor komposit ialah keupayaannya untuk dibahagikan dengan pelbagai faktor.
- Faktor ini menyumbang kepada pembahagi berbilang mereka melebihi satu dan nombor itu sendiri.
Kepentingan Pelbagai Pembahagi:
-
- Mempunyai berbilang pembahagi menandakan bahawa nombor bukan nombor perdana.
- Ia mempamerkan sifat “komposit” nombor – ia terdiri daripada pelbagai faktor.
Contoh Nombor Komposit:
-
- Sebagai contoh, ambil nombor 15. Ia boleh dibahagikan sama rata dengan 3 dan 5 (selain 1 dan 15), menjadikannya nombor komposit.
- Contoh lain ialah 28, yang boleh dibahagikan dengan 2, 4, 7, dan 14, mendedahkan sifat kompositnya.
Jenis Nombor Komposit:
Kaedah untuk mengkategorikan nombor komposit melibatkan mengenal pasti nombor yang mempunyai dua faktor perdana, yang dipanggil “faktor perdana.” Nombor ini boleh menjadi separa perdana (separuh perdana) atau 2-hampir perdana, di mana pengganda mungkin sama (termasuk kuasa dua nombor perdana). Kategori lain, nombor sfenik, terdiri daripada nombor komposit dengan tiga pengganda yang berbeza. Kadangkala, adalah penting untuk membezakan antara nombor komposit dengan kiraan ganjil bagi pengganda perdana yang berbeza dan nombor yang mempunyai kiraan genap. Perbezaan ini adalah relevan, terutamanya untuk kategori yang terakhir.
Separuh Perdana (Separuh Perdana):-
Persamaan: \( n = p \cdot q \) dengan \( p \) dan \( q \) ialah nombor perdana yang berbeza.
2-Hampir Perdana:-
Persamaan: \( n = p^2 \) dengan \( p \) ialah nombor perdana.
Nombor Sfenik (Nombor Komposit Dengan Tiga Faktor Perdana Yang Berbeza):
Persamaan: \( n = p \cdot q \cdot r \) dengan \( p \), \( q \), dan \( r \) ialah nombor perdana yang berbeza.
Komposit Darab Ganjil:
Persamaan: \( n = p_1^{a_1} \cdot p_2^{a_2} \cdot \ldots \cdot p_k^{a_k} \) dengan \( p_1, p_2, \ldots, p_k \) ialah nombor perdana yang berbeza dan \ ( a_1, a_2, \ldots, a_k \) ialah integer ganjil.
Komposit Darab Genap:
Persamaan: \( n = p_1^{a_1} \cdot p_2^{a_2} \cdot \ldots \cdot p_k^{a_k} \) dengan \( p_1, p_2, \ldots, p_k \) ialah nombor perdana yang berbeza dan \ ( a_1, a_2, \ldots, a_k \) ialah integer genap .